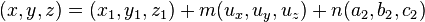Plano (geometría):

En geometría, un plano es un objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas; es un concepto fundamental de la geometría junto con el punto y la recta.

Son las que situadas en un plano se cortan en un punto.

Las rectas A y B de la siguiente figura se cortan en el punto C. Estas rectas se dice también que son concurrentes o convergentes que significa que tienden a unirse o que la distancia entre ellas se va haciendo menor hasta cortarse en un punto

Propiedades del plano ℝ³

Dos planos o son paralelos o se intersecan en una línea.En un espacio euclidiano tridimensional ℝ³, podemos hallar los siguientes hechos, (los cuales no son necesariamente válidos para dimensiones mayores).

Una línea es paralela a un plano o interseca al mismo en un punto o es contenida por el plano mismo.
Dos líneas perpendiculares a un mismo plano son necesariamente paralelas entre sí.
Dos planos perpendiculares a una misma línea son necesariamente paralelos entre sí.
Entre un plano Π cualquiera y una línea no perpendicular al mismo existe solo un plano tal que contiene a la línea y es perpendicular al plano Π.
Entre un plano Π cualquiera y una línea perpendicular al mismo existe un número infinito de planos tal que contienen a la línea y son perpendiculares al plano Π

LÍNEAS CONVERGENTES

Son las que saliendo de dos puntos del mismo plano, a medida que avanzan se juntan en un punto dado:

Como ves, las rectas han salido de los puntos A y B y si se prolongan, se juntarán en C.

LÍNEAS DIVERGENTES

Son las que saliendo del mismo punto, a medida que avanzan se van separando una de otra:

Divergir o separarse es lo contrario de convergir.

15.19 ¿Dos rectas convergentes pueden llegar a cortarse?

Respuesta: Sí, siempre que se las alarguen convenientemente.

15.20 Dos o más rectas secantes ¿podemos decir que son convergentes?
Respuesta: Sí, porque las rectas secantes se cortan y por ello han convergir, dirigirse a un punto.

RECTAS QUE SE CRUZAN

Las rectas que se cruzan están en distintos planos y por lo que no tienen ningún punto en común. Nunca se encuentran.

Las rectas que tienes a la izquierda en color azul están situadas en planos diferentes y comprobarás que no tienen, por mucho que se prolonguen, ningún punto en común

Ecuación del plano

Un plano queda definido por los siguientes elementos geométricos: un punto y dos vectores:

Punto P = (x₁, y₁, z₁)
Vector u = (u_x, u_y, u_z)
Vector v = (a₂, b₂, c₂)

(x,y,z)= (x_1, y_1 ,z_1)+ m(u_x, u_y ,u_z) +n(a_2, b_2 ,c_2) \,\!

Ejercicios:

1) Halla el ángulo que forman las rectas:
$r \equiv \left\{ \begin{array}{ll} x = 3-2t \\ y = 7+t \end{array} \right.$
$s \equiv \left\{ \begin{array}{ll} x = 1-4t \\ y = 4+3t \end{array} \right.$

SOLUCIÓN:

El ángulo entre dos rectas es el determinado por sus vectores directores.
Los vectores directores son $\vec{u_r}=(-2,1)$ y $\vec{v_s}=(-4,3)$
Si llamamos $\alpha$ al ángulo que forman y usamos la definición de producto escalar:
$\vec{u} \cdot \vec{v} = |\vec{u}| \cdot |\vec{v}| \cdot cos(\alpha)$ , podemos despejar el coseno:
$cos(\alpha) = \frac{\vec{u} \cdot \vec{v}}{ |\vec{u}| \cdot |\vec{v}|}= \frac{(-2)\cdot (-4)+1 \cdot 3}{\sqrt{(-2)^2+1^1} \cdot \sqrt{(-4)^2+3^2}}= \frac{11}{\sqrt{5} \cdot 5}$

Por tanto, $\alpha = arc \: cos \left(\frac{11}{\sqrt{5} \cdot 5 \right)$
$\alpha \cong 10.3$ grados

2) Halla el área del triángulo determinado por los puntos

SOLUCIÓN:

El área de un triángulo viene determinada por la fórmula $A = \frac{base \cdot altura}{2}$
Como base tomaremos el segmento $\overline{AB}$ y como altura tomaremos la distancia del punto

a la recta que pasa por

Calculamos la base = $|\vec{AB}| = \sqrt{(5-0)^2+(2-0)^2} = \sqrt{29}$
Ecuación de la recta que pasa por los puntos

Punto:

Vector: $\vec{AB} = (5,2)$
Ecuación continua: $\frac{x-0}{5}=\frac{y-0}{2}$
Pasamos a ec. general:

Aplicamos la fórmula de la distancia de un punto a una recta:

$d(C,r_{AB}) = \frac{|2 \cdot 1 - 5 \cdot 6|}{\sqrt{2^2+5^2}} = \frac{28}{\sqrt{29}}$

Finalmente calculamos el área:

$A = \frac{\sqrt{29} \cdot \frac{28}{\sqrt{29}}}{2} = \frac{28}{2} = 14$

El área es de 14 unidades cuadradas (

)

3) Dada la ecuación continua de una recta:

$\frac{x-2}{3} = \frac{y+1}{4}$ se pide:

dos puntos de la recta

dos vectores directores

representación gráfica

SOLUCIÓN

La propia ecuación continua ya nos aporta el punto

Para obtener más puntos de la recta, basta con darle valores a

e ir calculando

(o al revés).
Para

tenemos $\frac{0-2}{3} = \frac{y+1}{4}$
$(-2) \cdot 4 = 3 (y+1)$

Por tanto un segundo punto sería

Un vector director de la recta sería el que nos aporta los denominadores de la propia ecuación continua $\vec{v}=(4,3)$ . Cualquier vector proporcional al anterior valdría como vector directo de la recta, por ejemplo $\vec{u}=(8,6)$

Para dibujar la recta, bastaría con dibujar los dos puntos que conocemos de la misma y a continuación trazar la recta.

Geometría en el Plano

martes, 24 de mayo de 2016

Geometría en el Plano.

Plano (geometría):

Propiedades del plano ℝ³

Ecuación del plano

SOLUCIÓN:

SOLUCIÓN:

SOLUCIÓN

martes, 24 de mayo de 2016

Geometría en el Plano.

Plano (geometría):

Propiedades del plano ℝ3

Ecuación del plano

SOLUCIÓN:

SOLUCIÓN:

SOLUCIÓN

Propiedades del plano ℝ³